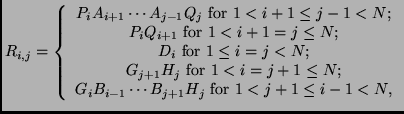
Pattern:
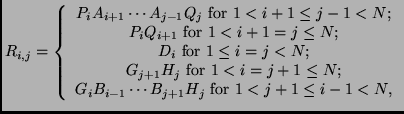
Properties: principal off-diagonal submatrices of
low rank, unified description for the structure of band
matrices and inverses of
band matrices
Source/utilization: test for linear system solvers and
for the computation of the eigenvalues
References
Y. Eidelman and I. Gohberg,
Integral Equations and Operator Theory, 34(1999), 293-324